Understand the limits of your data and beware of extrapolation. This point deserves endless repetition because uncritical acceptance of computer output contributes to many process problems.
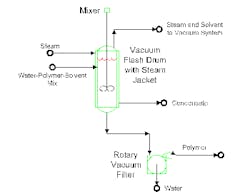
One recent example involves solvent removal from water/polymer slurry. The proposed system (Figure 1) uses a vacuum flash to eliminate residual solvent from the slurry. The solvent/polymer stream mixes with water. After decanting, the mixture enters a flash vessel. The heated flash drives solvent and water vapors to a vacuum system. The water/polymer mixture goes to a rotary vacuum filter for final separation of polymer from water.
The purpose of the vacuum flash is to reduce solvent concentration to 50 ppm in the water slurry mixture. Steam in the jacketed flash drum provides heat for solvent vaporization.
The designers used a standard commercial simulator and its default settings for the water/solvent flash. To check the results, they located literature values for Henry's law coefficients for the system.
Henry's law states that the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas. However, significant deviations occur, especially at low concentration levels.
Commonly, Henry's law is written as:
Ki = yi/xi = Hi/Ptotal
where Ki is the partial coefficient, yi is the mole fraction of species i in the vapor phase, xi is the mole fraction of species i in the liquid phase, Hi is the Henry's law constant, and Ptotal is the total pressure of the system.
In this case, plugging in the Henry's law vapor pressures provided significantly different results than the simulation. For instance, at 1 psig and 140°F, the model gave a solvent concentration in water of 2,147 wppm compared to 10,809 using the Henry's law literature data; at 108°F, results were 2,076 versus 20,751. In general, using data from low concentration ranges tends to show separations are more difficult than extrapolations from high concentration ranges indicate. However, this isn't always true.
Besides giving a much higher amount of solvent in the feed, the calculations based on literature data exhibited a much stronger temperature dependence than the simulator extrapolations — and the temperature effect was in the opposite direction. A check of multiple literature values showed a variation of approximately 17% for Henry's Law constants from different methods but all data agreed on the general trends.
Using the simulator results poses severe consequences for the vacuum system at the 140°F operation selected. Table 1 compares the differences in vacuum system load. Absolute pressure doesn't vary much because water partial pressure dominates the system. However, the required partial pressure of solvent differs significantly. The data-based results give a much higher solvent concentration in the feed — increasing the amount of solvent that must be removed by five times. The lower partial pressure of solvent in the vacuum flash boosts the water load to the vacuum system by more than twenty-fold. Together, these effects greatly raise the water vapor load on the vacuum system and the corresponding duty on the vacuum flash vessel.
The impact on the vacuum system actually exceeds the difference in total vapor rate above due to the shifting composition and much greater relative flow rate of low-molecular-weight water in the vapor stream. Using the correct basis gives 25 times the duty load for the heated jacket and vacuum system pre-condenser. The rest of the vacuum system is merely five times larger.
One other caution needs to be highlighted here. Most data for solvent in water are measured at very low solvent concentrations. The upstream atmospheric flash has an around 80% solvent concentration in the flash vapor. This is a completely different operating region that requires checking against suitable data.
Don't use data methods in simulations outside the ranges upon which they are based. Remember that extrapolation to ppm levels often creates problems. And always perform a reality check on any computer results.
Andrew Sloley is a Chemical Processing Contributing Editor. You can e-mail him at [email protected]. You can e-mail Scott Henson at [email protected].