Plant InSites: Come Up With a Solid Estimate
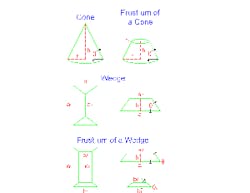
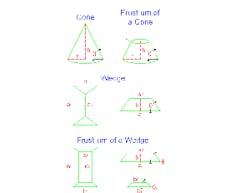
Large-scale solids-handling operations often rely on storing material in piles. The pile layout and solid's properties set the volume storable in a given area. Piles most often approximate one of four common shapes: a cone: a frustum of a cone; a wedge; or a frustum of a wedge (Figure 1) — a frustum essentially is the underlying shape with its top cut off.
where h is the height and r is the radius.For a frustum of a cone, the volume is:v = πh(r12 + r22 + r1r2)/3(2)
where r2 = r1 – h/tan Θ.For a wedge, the volume is:
v = hb(2a1 + a2)/6 = hb[3a1 – 2h/tan Θ]/6 (3)
where a2 = a1 – 2h/tan Θ1.
For a frustum of a wedge, the volume is:
v = h[a1b1 + (a1 + a2)(b1 + b2) + a2b2]/6 (4)
where b2 = b1 – 2h/tan Θ2.
You can use these equations, which apply both to unconstrained piles and bulk solids flowing in constrained spaces such as hoppers, with those for other standard shapes to determine a variety of volumes.
Andrew Sloley is a Chemical Processing contributing editor. You can e-mail him at [email protected].
Table 1. This list presents reasonable values for the materials but actual value can vary markedly depending upon application.
| Material | Θ, degrees |
| Activated carbon | 20-29 |
| Alfalfa, meal | 45 |
| Alfalfa, pellets | 9 |
| Alumina | 22 |
| Anthracite ash | 45 |
| Barley | 30 |
| Bauxite | 31 |
| Carbon black | 25 |
| Caustic soda | 29-43 |
| Cement | 37-40 |
| Cinders, bituminous coal | 25-41 |
| Clay, soft | 10 |
| Clay, compacted | 10-25 |
| Coal, anthracite | 27 |
| Coal, bituminous | 35 |
| Coke, lose pile | 30-45 |
| Corn | 23 |
| Diatomaceous earth, calcined | 30-44 |
| Flaxseed | 21 |
| Gravel, round | 30 |
| Gravel, sharp | 40 |
| Gypsum | 30 |
| Iron Ore | 35-45 |
| Limestone, pulverized | 30-44 |
| Lime, hydrated | 40 |
| Linseed | 25 |
| Millet | 23-25 |
| Phosphate rock, crushed | 25-29 |
| Phosphate rock, ground | 40 |
| Plastic resin grains, cellulose acetate | 16 |
| Plastic resin grains, fluorocarbon | 6 |
| Plastic resin grains, nylon | 9 |
| Plastic resin grains, polyethylene pellets | 23 |
| Plastic resin grains, vinyl | 10 |
| Plastic resin grains, viscose | 10 |
| Oats, rolled | 30-44 |
| Quartz, ½-in. screenings | 20-29 |
| Quartz, 1.5-3 in. | 30-44 |
| Rapeseed | 18-22 |
| Rice | 30-44 |
| Safflower | 24 |
| Salt | 36 |
| Sand, dry | 25-35 |
| Sand, moist | 30-45 |
| Sand, wet | 20-40 |
| Scrap metal | 35-45 |
| Silt, compacted | 25-40 |
| Silt, loose | 20-30 |
| Sand-clay, compacted | 40-50 |
| Soda ash, dense | 32-42 |
| Soda ash, light | 59 |
| Sulfur, granules | 35 |
| Sunflower seed | 23 |
| Wheat, whole | 28 |
| Wheat, cracked | 30-44 |
| Wood chips | 45 |